They first train an encoder that summarizes the reasoning up to a checkpoint. They call it enc.

Assume we have a question $X$ and a reasoning chain that we split into chunks $S_i$. So the whole thing looks like this: $[X,S_0,S_1,\cdots,S_N, Ans]$. The encoder should get the input $[X,S_0,S_1,\cdots,S_i,L]$ and produce a summary we call $Z_i$. This $Z_i$ should have the property that we can replace those chunks with $Z_i$ and the LLM can still continue the reasoning chain. So the LLM should be able to produce $[S_{i+1}, S_{i+2}, \cdots, S_n, Ans]$ given $[X, Z_0, Z_1, \cdots, Z_i]$. This is considered a good summary.

They first argue that these $Z_i$s should lie in the linear space of the input token embeddings, since the LLM only knows how to interpret that space (Section 3). So they designed enc to produce logits normally given $[X,S_0,S_1,\cdots,S_i,L]$, and then $Z_i$ is the linear combination of the predicted tokens.

Training the enc and LLM models

To train these models, they use the following loss:

$$\ell_{\text{sup}} = \frac{1}{N} \sum_{i=1}^{N} \frac{1}{

J_i

} \sum_{t \in J_i} (-\log p_{\theta}(x_t

{I}_i; \text{LTSuM}))$$.

$J_i$ is the set of indices of tokens in chunk $i$. $N$ is the total number of chunks, and $p_{\theta_{LLM}}(x_t | {I}_i; \text{LTSuM})$ is the probability that the model gives the correct token $x_t$ given the previous summaries $[X, z_0, z_1, \cdots, z_i]$. So it measures how well the model predicts the future tokens given the $Z_i$s. Note that in this phase the model is not given the previous chunks’ actual text, only the summaries.

However, $\theta_{enc}$ is used to generate $Z_i$s given the previous context. So to generate $L_i$ the model sees $X, S_0, \cdots, S_i$, but not any $L_i$.

So in the above loss we have two different models, enc and LLM, involved, but they have separate caches and everything. The only way enc affects that loss is through the $Z_i$s.

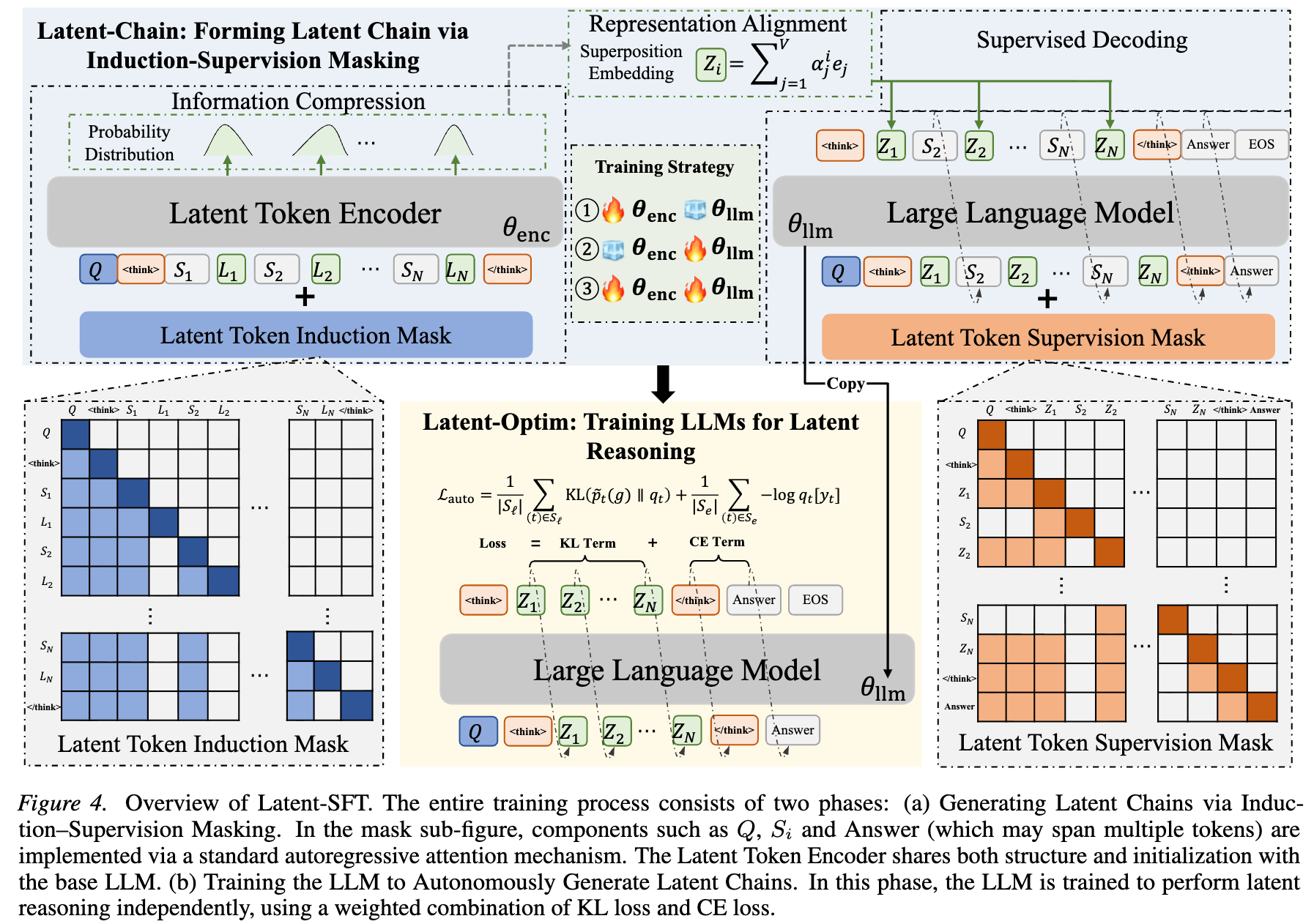
Training a latent reasoning model using $Z_i$s

They then use enc to compress/translate some CoT data (problem + reasoning + answer) into the $[X, Z_0, \cdots, Z_N, Ans]$ format. They also save the $\alpha_i$ values that generated those $Z_i$. These $\alpha_i$ will be used as the targets of the latent reasoning model.

They train the model using normal SFT loss for the explicit part and another loss for the latent part.

\[L_{\text{auto}}(\theta_{\text{llm}}) = L_{exp}(\theta_{\text{llm}}) + L_{lat}(\theta_{\text{llm}}).\]

We have

\[L_{exp}(\theta_{\text{llm}}) = \frac{1}{|S_{\text{exp}}|} \sum_{t \in S_{\text{exp}}} (-\log q_t[y_t])\]

This is normal SFT on normal data.

For the latent part they add noise to $\alpha_i$ like this: $\tilde{p}_t = \text{softmax} \left( \log \alpha_t + g_t \right) \quad g_t \sim \text{Gumbel}(0, 1)$. They then do a somewhat normal SFT on them.

\[L_{lat}(\theta_{\text{llm}}) = \frac{1}{|S_{\text{lat}}|} \sum_{t \in S_{\text{lat}}} \mathbb{E}_{\mathbf{g}} \left[ \text{KL}(\tilde{p}_t(\mathbf{g}) \,\|\, \mathbf{q}_t) \right]\]

Model compresses a reasoning path

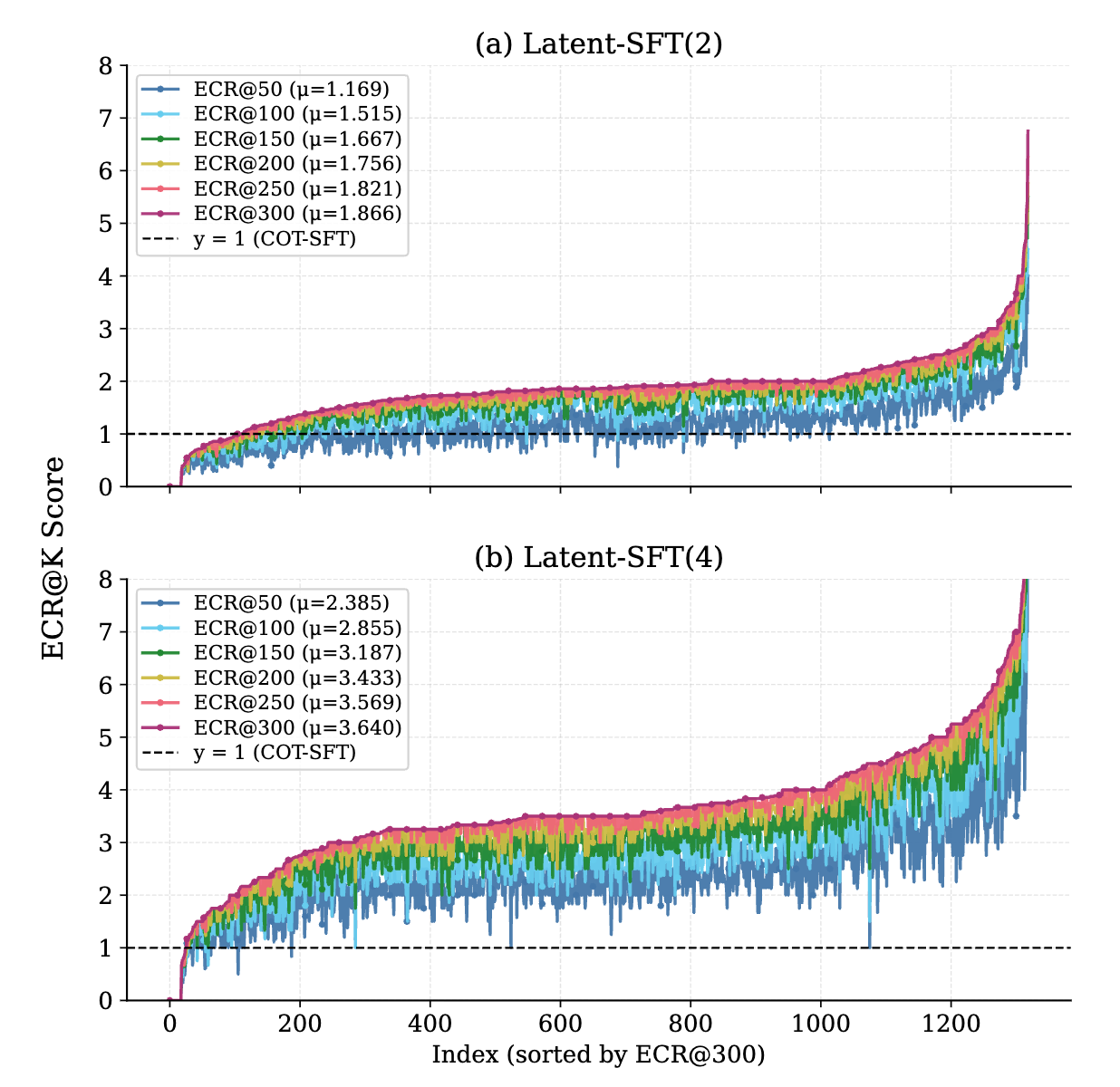
In this part their figures and arguments are reasonable. They show that in the top 50 tokens in the $\alpha_i$ they have many tokens of $S_i$. They have $1.169$ on average when each chunk has two tokens, and $2.385$ on average when each chunk has four tokens. So it is reasonable to assume that the model is doing the same reasoning path but faster.

Model doing multiple reasoning paths

They manually made several reasoning paths for GSM8K problems.

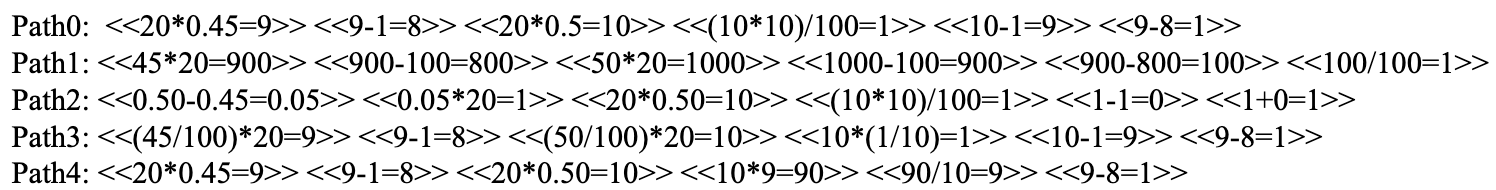
They measure how much the latent reasoning path intersects with these different paths and calculate a sum-like metric. They show this value is larger than 1.7 for most samples. They argue this is the number of parallel reasoning paths the model follows.