Certified Robust Neural Network

Certify Robustness using median neurons

L-inf dist neurons are introduced by zhang2021towards. With this neuron, they have achieved superior certified accuracy on various datasets, including CIFAR-10.

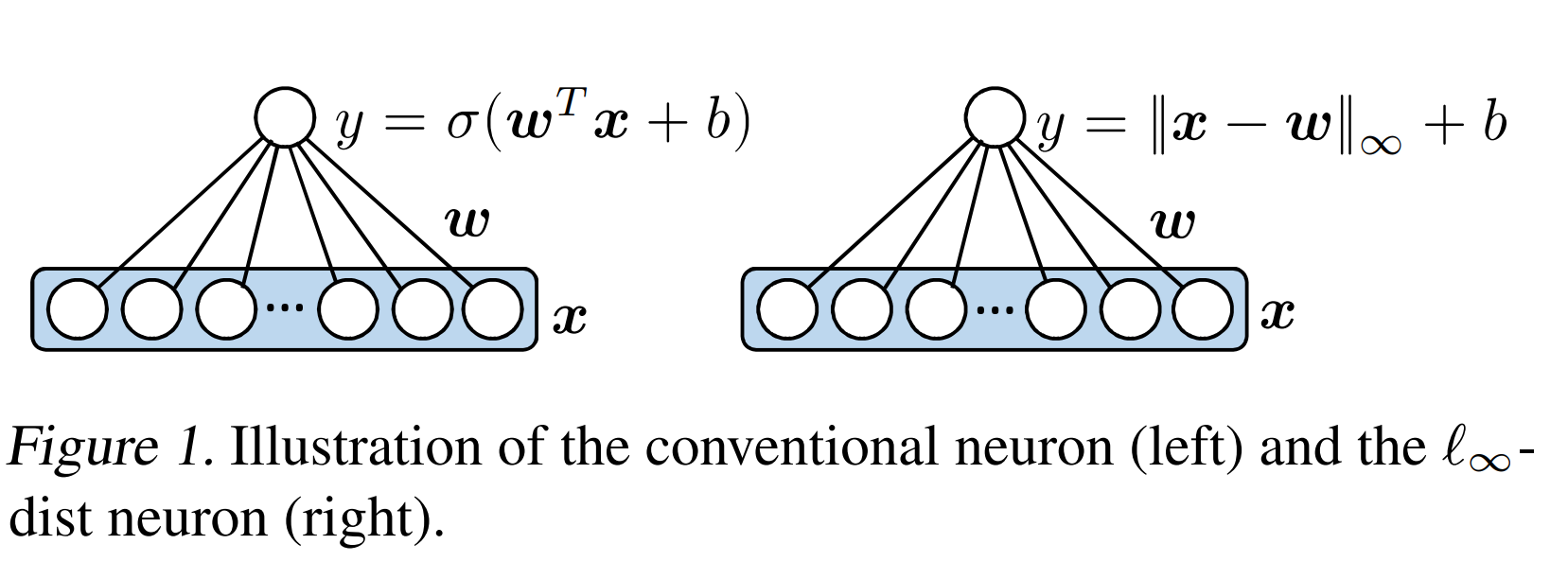
This illustration shows how an L-inf distance neuron works.

As shown in the illustration, each neuron calculated the L-inf dist of its input to some learnable point, plus a fixed constant. With this formulation, the Lipschitz of each neuron output with respect to its input is \(1\); Therefore, each layer Lipschitz is equal to \(1\), and further, the whole network is Lipschitz one. Lipschitz’s networks could easily certify their robustness under L-inf perturbations.

In the first experiment, I discovered that this network could be pruned by a staggering 98% without any loss in accuracy or certified accuracy.

The sparsification of an L-Inf distance neuron, where only certain dimensions are considered, effectively reducing the edges by 98%.

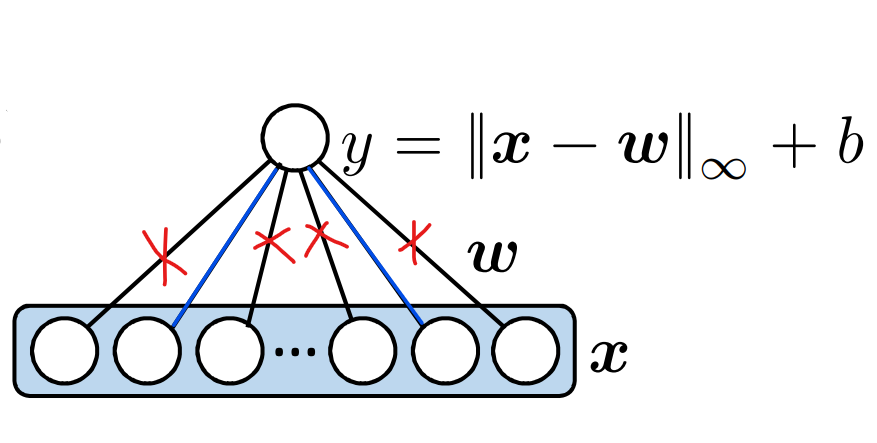
As depicted above, the neurons calculate the L-inf distance only along certain dimensions, while others are ignored. In this visualization, each dimension corresponds to an edge in the graph, illustrating a substantial reduction of 98% in connections without compromising accuracy or certified accuracy.

The approach in which we chose edges to remove was straightforward. Using the training dataset, we count how many samples a specific edge causes the L-inf distance change. L-inf distance could be seen as a max function on absolute values. Mathematically
\(\| W \| = max(\|W_i\|)\)
So in each Maximum, we checked which element matters. After this calculation, we remove edges that counted less than a specific constant.

This work raises an interesting question if this network does not use its total capacity, what happens if it does? It is an essential question since it has been proved that robustness needs more parameters, and if our network does not use its total capacity, it somehow means it has fewer parameters. To mitigate this issue, I proposed median-neuron, which calculates \(y=median(X_i-W_i)+b\) instead of \(y=max(\|X_i-W_i\|)\). At first, it seems this neuron could get higher accuracy and robust accuracy since the median is a robust function by its nature. Nevertheless, we were not able to train this network properly.

In addition to the median, we tried \(r\)-the element in the sorted array function. It means each neuron has a learnable \(R\), and its output is calculated as follows

$$y=(Sorted(X_i-W_i)_R)+b$$

to make these \(R\)s learnable, we should apply some normalization to the \(R\)-th element function; Therefore, during training, we applied

$$y=\sum_{i} {Sorted_i(X_j-W_j)}{T(\|R-i\|)}+b$$

In which T is a decreasing function. By making T steeper, we converge to the \(R\)-th function.

The code is available on GitHub.